A lei de Gauss para a eletricidade afirma que o fluxo de campo elétrico através de uma superfície fechada qualquer é igual à carga elétrica total no interior dessa superfície dividida pela constante ε0. Matematicamente:
Σk = 1, 2 … N Ek • Δsk = q/ε0 [Superfície Fechada]
Vamos usar essa lei para determinar o campo elétrico gerado por uma partícula com carga elétrica Q. Como superfície fechada, vamos escolher uma superfície esférica em cujo centro se encontra a partícula carregada.
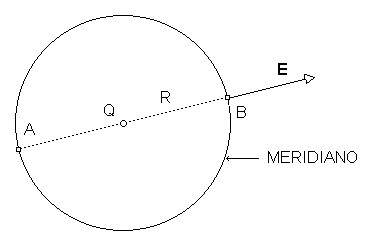
A figura representa um meridiano da superfície esférica escolhida. O segmento A-B é um diâmetro qualquer. A carga Q concentra-se numa pequena região no centro da superfície esférica, isto é, onde se encontra a partícula carregada. Por simetria, o vetor campo elétrico E no ponto B não pode ter qualquer componente perpendicular ao diâmetro A-B. Assim, exatamente como está representado na figura, o vetor campo elétrico no ponto B é radial, isto é, tem a direção do diâmetro (A-B). O mesmo argumento pode ser repetido para qualquer outro diâmetro desse e de outro meridiano qualquer e a conclusão que chegamos é que o vetor campo elétrico, em qualquer ponto da superfície esférica, é perpendicular ao elemento de superfície local.
Além disso, como todos os pontos da superfície esférica estão igualmente espaçados da partícula carregada central, todos os vetores de campo elétrico em todos os pontos da superfície esférica têm módulos iguais.
Por outro lado, o vetor campo elétrico E representado na figura aponta para fora da superfície, correspondendo a uma carga Q positiva.
Agora, imaginemos a superfície esférica dividida em um grande número N de elementos de superfície, com áreas Δsk (k = 1, 2, … N), pequenos o suficiente para que, sobre cada um deles, o campo elétrico possa ser considerado constante.
Por convenção, cada um dos vetores Δsk é perpendicular ao correspondente elemento de superfície e aponta para fora da superfície esférica. Assim, em cada elemento de superfície, os vetores Δsk e Ek são paralelos.
Por tudo isso e pelo fato de que a área da superfície esférica é 4πR2, temos:
Σk = 1, 2 … N Ek • Δsk = E Σk = 1, 2 … N Δsk = E (4πR2)
Com esse resultado, a expressão matemática da lei de Gauss para a eletricidade fica:
E (4πR2) = Q/ε0
e daí:
E = (1/4πε0) Q/R2
Este é o módulo do vetor campo elétrico a uma distância R da partícula com carga Q. A direção do vetor é radial e o sentido, de afastamento da partícula, se Q é positiva, e de aproximação, se Q é negativa.

As figuras representam as linhas de campo elétrico de partículas carregadas positiva e negativamente.
