Quando um sistema percorre um ciclo de Carnot, com um reservatório térmico mantido à temperatura baixa T₁ e um reservatório térmico mantido à temperatura alta T₂, independentemente da substância que forma o sistema, vale a relação:

T₂/T₁ = − Q₂/Q₁

em que Q₁ é a quantidade de energia trocada entre o sistema e o reservatório mantido à temperatura T₁ e Q₂ é a quantidade de energia trocada entre o sistema e o reservatório mantido à temperatura T₂. Aqui, T₁ e T₂ são temperaturas na escala kelvin.

Indicando uma soma por meio da letra grega Σ, podemos escrever a expressão acima como:

Σ_{k = 1, 2}  Q_k/T_k = 0

Um ciclo reversível C qualquer pode ser pensado como composto de certo número N de ciclos de Carnot, todos percorridos no mesmo sentido, como indicado na figura. As porções adiabáticas de ciclos adjacentes, que coincidem, como E-F, por exemplo, são percorridas duas vezes, em sentidos contrários (como indicado pelas setas), e seus efeitos cancelam-se mutuamente.

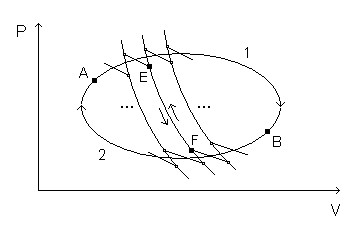
As porções isotérmicas e as porções adiabáticas não canceladas constituem um ciclo, que denotaremos por Z e que aparece como uma linha em ziguezague no plano PV. Para esse ciclo Z, podemos escrever:

Σ_{k = 1, 2 … 2N}  (Q_k/T_k)_z = 0

Nesta expressão, os termos do somatório estão relacionados às porções isotérmicas do ciclo Z.

Se o número de ciclos de Carnot aumenta, existe um cancelamento mais completo dos efeitos das porções adiabáticas. Se tomarmos um número de ciclos de Carnot muito grande, o ciclo Z se confunde com o ciclo original C, as quantidades de energia trocadas entre o sistema e a vizinhança por calor se tornam muito pequenas (e são simbolizadas por ΔQ) e o seu número se torna muito grande. Nesse caso, escrevemos:

Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_c = 0

Por outro lado, consideremos dois estados A e B arbitrários sobre o ciclo C. Nesse caso, o ciclo C pode ser considerado como formado pelos processos A-1-B e B-2-A. Da expressão acima, podemos escrever:

Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_A1B + Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_B2A = 0

O ciclo C é reversível. Portanto, o processo B-2-A pode ser percorrido em sentido contrário, de modo que:

Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_B2A = − Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_A2B

e a expressão anterior fica:

Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_A1B = Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_A2B

Colocando esse resultado em palavras, podemos escrever o seguinte: a soma das quantidades ΔQ_k/T_k tem o mesmo valor, seja ela feita para o processo reversível A-1-B ou para o processo reversível A-2-B. Como podemos repetir todo o argumento para qualquer outro ciclo reversível que passe pelos estados A e B, concluímos que a soma das quantidades ΔQ_k/T_k é a mesma, independentemente do processo reversível que leva o sistema do estado A para o estado B. Na verdade, temos aqui duas idéias diferentes, que podem ser representadas matematicamente pelas seguintes expressões:

ΔS = S_B − S_A

ΔS = Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_AB          [Processos Reversíveis]

A primeira expressão indica que, quando o sistema passa do estado A para o estado B, uma propriedade sua, representada pela letra S, tem uma variação que depende apenas do estado A e do estado B e não do processo que o sistema desenvolve entre esses estados. Essa propriedade é chamada entropia. Como a entropia depende apenas dos estados A e B, ela é uma função de estado.

A segunda expressão indica que, se o processo pelo qual o sistema é levado do estado A para o estado B é reversível, a variação da entropia do sistema é dada pelo somatório à direita da igualdade.

Vamos discutir agora, com a ajuda da expansão livre de um gás ideal, o caso em que o sistema é levado do estado A para o estado B por um processo irreversível.

Dois recipientes, 1 e 2, são conectados com uma válvula fechada. No recipiente 1 existe certa quantidade de gás ideal num estado de equilíbrio A e no recipiente 2 existe vácuo (figura (a)). Ambos estão isolados da vizinhança.

Quando abrimos a válvula, a amostra de gás ideal se expande pelo recipiente 2 e o gás, depois de certo tempo, alcança um estado de equilíbrio B.

A expansão livre do gás, do estado A para o estado B, é um processo irreversível porque não é quase-estático. Como os estados A e B são diferentes, suas entropias são diferentes. Para calcular a diferença de entropia entre esses estados, podemos imaginar um processo reversível que leve o gás do estado B de volta ao estado A (figura(b)).

No processo A → B, a pressão do gás diminuiu, mas sua temperatura T permaneceu constante. Então, o processo B → A pode ser um processo de compressão lenta, mantendo a temperatura T constante. Para que isso aconteça, o gás deve ceder uma quantidade Q de energia por calor para a vizinhança. Dessa forma:

ΔS = S_A − S_B = (1/T) Σ_{k = 1, 2 … ∞}  (ΔQ_k)_BA = Q/T

Mas, conforme a convenção que estamos usando, Q < 0 quando a energia por calor passa do sistema para a vizinhança. Desse modo, fazendo Q = − |Q| podemos escrever, da expressão acima:

S_B = S_A + |Q|/T

Em palavras: a entropia do gás ideal aumenta com a expansão livre (que é um processo irreversível).

De modo geral, e coletando uma expressão desenvolvida acima:

ΔS = Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_AB          [Processos Reversíveis]

ΔS > Σ_{k = 1, 2 … ∞}  (ΔQ_k/T_k)_AB          [Processos Irreversíveis]

Se o sistema está isolado, todos os ΔQ_k são nulos e então:

ΔS = 0          [Processos Reversíveis]

ΔS > 0          [Processos Irreversíveis]

Leis da Termodinâmica